3.      Structuration spatiale et autocorrélation spatiale

Une des étapes centrales de notre projet a été de parvenir à une base de données homogène permettant de procéder à un examen systématique de la structuration spatiale. Elle se fonde précisément sur les résultats agrégés dont nous disposons, offrant à l’étude des échantillons à la fois plus robustes d’un point de vue statistique, de taille raisonnable en matière de calculabilité et enfin d’une répartition spatiale équilibrée et à ce titre représentative de l’espace sud-indien.

La présente section résume certains des résultats et des conclusions les plus intéressantes de cette étude. Nous souhaitons toutefois souligner en amont notre choix d’outils géostatistiques. Nous allons ici recourir avant tout aux indices de Moran. La statistique de Moran est la plus classique et très proche de l’indice de Geary, utilisé également pour mesurer l’association spatiale. On notera en outre que Moran a l’avantage de se décliner en indice local, dont on tirera parti plus loin dans l’analyse. Il demeure que nos calculs auraient pu être présentés à partir d’indicateurs différents sans que cela ne nuise à notre raisonnement.

L’indice de Moran mesure le degré d’autocorrélation spatiale sous forme d’autocovariance relative des observations pour une variable z. La covariance relative n’est autre que le produit moyen des valeurs observées (et centrées sur la moyenne) rapporté à la variance de l’échantillon. Quand la variable est normalisée (moyenne = 0 et σ²=1), la covariance relative n’est que la moyenne des produits croisés des valeurs de la variable z. On parlera ici d’autocovariance pour tenir compte du fait que les produits sont calculés pour une même variable, mais pour différentes observations. On aura toutefois noté l’analogie avec le coefficient de corrélation, qui rapporte la covariance entre deux variables au produit de leur écart-type.

 La définition classique de l’indice de Moran, appliqué à des observations i et j, dépend d’une matrice de proximité notée Wij, prenant la valeur 0 partout sauf pour les i et j voisins.

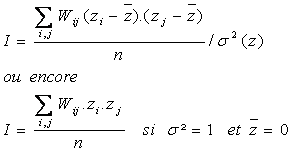
Une extension de cette formule consiste à définir différentes classes de voisinages ; la matrice Wij(d_k) prendra désormais la valeur 1 quand i et j seront distants de d_k. On examinera alors de manière régulière l’évolution de I(dk), de d₁ à d_m (distance à laquelle l’autocorrélation devient négligeable), au moyen d’un corrélogramme.

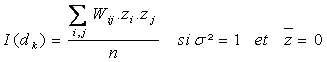
Cette écriture permet d’entrevoir des calculs détaillés de Moran par classe de distance croissante, plutôt que pour les seuls voisins (espaces directement contigus). Le comportement de la variable z est alors décrit sur des rayons croissants.

Une définition supplémentaire reprend la classe des voisinages simples, divisant simplement l’ensemble des paires d’observations en « voisins » et « non-voisins ». Toutefois, le calcul de Moran est déséquilibré, car certaines observations sont plus représentées que d’autres : certaines localités centrales ont en effet plus de voisins que d’autres, situées par exemple sur les limites du territoire ou dans des zones éparses. On choisit alors de corriger ce biais en calculant un indice Moran corrigé du nombre variable de localités prises en compte, imposant donc un poids identique à chaque observation.

La définition classique de l’indice de Moran considère en effet que plus le nombre de voisins est important, plus l’individu aura de poids dans la matrice de pondération. Le nombre de paires de voisins (m) est alors égal à. Cela ne se justifie que rarement. Au contraire, on préfère que chaque individu ait le même poids, c’est-à-dire que sa contribution à l’indice d’autocorrélation spatiale soit la même, qu’il ait un ou plusieurs voisins. Pour cela, il faut standardiser la matrice en ligne (row standardization). Cette opération consiste à pondérer le nombre de voisins j de chaque localité i pour que chaque ligne de la matrice (qui décrit les voisins de chaque individu i) soit égale à 1. En d’autres termes, si un point a 5 voisins, chaque voisin comptera pour 1/5^ème du total. Dans ce cas, le nombre de paires de voisins (m) est égal au nombre des localités i (n), comme si chaque individu n’avait qu’un voisin.

3.1.   Les principales dimensions : autocorrélation spatiale et distance

Pour un premier examen, nous avons choisi d’utiliser l’indice de Moran par classe de distance. Les corrélogrammes obtenus sont alors assez simples à lire et décrivent en détail la structuration spatiale propre à la variable étudiée.

A titre d’exemple, le premier schéma fourni repose sur la variable de densité. Les unités d’observation sont ici les 2151 clusters ruraux de 10 km qui découpent l’Inde du Sud. Leur caractère statistique est relativement robuste en raison de leur taille moyenne, autant en termes de superficie que de population. Sur ce schéma, on lit la décroissance régulière de l’indice d’autocorrélation spatiale en fonction de la distance séparant les paires d’observations. Chaque point est la valeur de l’indice pour un pas de distance donnée.

Ces distances sont ici classées par pas de 20 km, distance suffisante pour le premier intervalle qui contient déjà 3000 paires. La distance exacte représentée est la moyenne des distances dans chaque intervalle, en général identique au milieu de l’intervalle. La distance maximale représentée est ici de 500 km, bien en retrait de la distance maximale entre les extrémités de l’Inde du Sud (distantes de 1500 km). Toutefois, il s’agit d’une limite suffisante, car l’autocorrélation spatiale mesurée par l’indice de Moran est systématiquement nulle ou négative au-delà de ce seuil comme nous le verrons plus bas.

Dans la lecture du corrélogramme, on distinguera notamment:

1.      le profil (ou la courbure), en général monotone décroissante

2.      la valeur maximale (à distance minimale), ici de 0,63, qui est en général le Moran du premier voisinage souvent utilisé pour résumer cet indice

3.      La portée, ici de 430 km, qui est le niveau auquel s’annule l’indice. L’indice de Moran en l’absence d’autocorrélation spatiale est de -1/(n-1), en l’occurrence -0.0004. Sur les gros effectifs, on considérera que l’indice est significatif au-delà de 0.1

4.      La courbure des indices correspondant à la vitesse à laquelle décroît l’indice. Cette courbure peut être linéaire, concave (comme ici), voire convexe.

 

Figure 5 : Indice de Moran calculé pour la densité sur des pas de 20

pour les clusters de 10 km

Le même protocole de calcul a été appliqué à un jeu de variables, choisies pour leur relative robustesse et leur exemplarité analytique. Il s’agit en fait d’indicateurs importants de la configuration socio-économique de l’Inde du Sud rurale, mais nous ne les détaillerons pas ici.

La premier graphique superpose l’indice de Moran par distance pour douze variables différentes. On observera en premier lieu la présence de trois variables qui se distinguent à la fois par des maxima très élevés (supérieurs à 0.8), une courbure linéaire ou faiblement concave et une portée très élevée. Deux d’entre elles (taille du ménage et rapport enfants-femmes) sont en réalité étroitement corrélées, dépendant toutes deux de manière endogène du niveau moyen de fécondité dans les localités. Le niveau d’alphabétisation, lui-même associé à la fécondité de manière exogène, se caractérise notamment par une portée maximale (supérieure à notre seuil de 500 km) qui traduit l’étalement extrêmement régulier du niveau d’instruction sur l’ensemble de la région. Ces trois indicateurs présentent donc la plus forte structuration spatiale, atteignant à faible distance des niveaux proches du maximum de 1. Si la décroissance est très rapide avec la distance, l’autocorrélation spatiale reste accusée à plus de 250 km, même en cas de franchissement de frontières administratives. L’interprétation de cette structuration spatiale propre aux comportements reproductifs et à la progression de l’éducation en zones rurales renvoie directement à des mécanismes de propagation du changement social ; il s’agit en effet de variables dynamiques associés à des phénomènes sociaux qui ont énormément évolué durant les cinquante dernières années (baisse de la natalité, progrès de l’instruction, nucléarisation familiale, etc.). Les effets propres à la diffusion spatiale de l’éducation ou du malthusianisme sont ici mis en évidence pour une analyse sociodémographique originale.

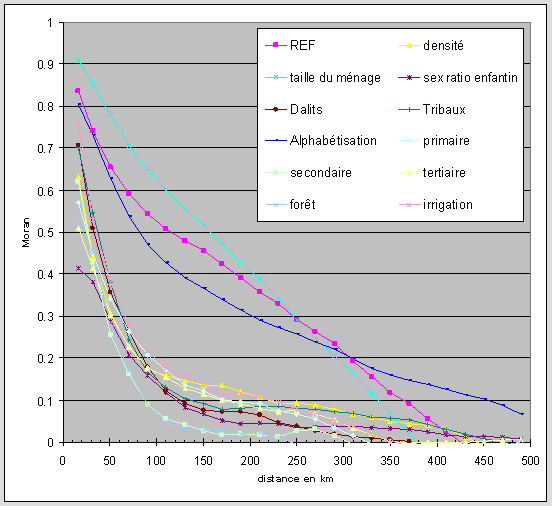
 Figure 6 : Indices de Moran calculés sur des pas de 20 pour les clusters de 10 km

Les neuf autres variables présentent une structuration spatiale moins affirmée. On notera que si les maxima peuvent être parfois très élevés parmi ces indicateurs, la décroissance avec la distance est presque verticale durant les premiers cent kilomètres. Nous avons donc ici affaire à des phénomènes qui sont beaucoup plus localisés. L’autocorrélation spatiale devient assez mineure avant 200 km.

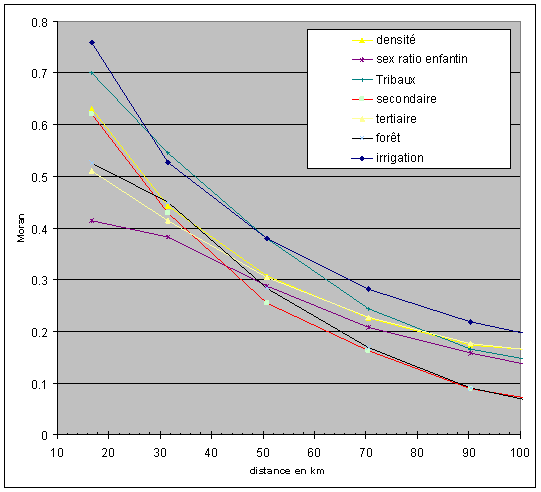
Figure 7 : Indices de Moran calculés sur des pas de 20 pour les clusters de 10 km (sélection)

La figure 7 suivante permet un examen plus fin de certaines d’entre elles. Nous y avons intentionnellement limité la distance à 100 km. On observe ainsi que certaines dimensions, comme la part de la main-d’œuvre dans le secondaire, se caractérise par une forte concentration spatiale à courte distance, mais qui disparaît très vite. Ceci décrit donc les formes d’implantation des activités industrielles ou semi-industrielles en zones rurales. L’étalement du tertiaire est, à titre comparatif, plus large. Parmi les variables du milieu, on notera la forte concentration de l’irrigation, mais une distribution moins concentrée du couvert forestier qui pourrait indiquer indirectement la fragilité des données. L’autocorrélation du couvert végétal devrait en effet être forte et il se pourrait que ce soit plutôt la nature de nos données, relevant de la classification par le Département forestier qui soit problématique.

Notons enfin la particularité du sex-ratio des enfants, avant tout déterminé par les discriminations de genre (foeticide féminin, infanticide ou surmortalité des petites filles). On sait par ailleurs la très forte concentration spatiale à l’échelle de l’Inde des poches de déséquilibres de genre, ainsi que l’existence de foyers de discrimination en Inde du sud, circonscrits en deux régions du Tamil Nadu. Le résultat obtenu est donc contre-intuitif, puisque la dépendance spatiale semble au contraire très faible. En réalité, cette mesure est éclairante puisqu’elle démontre qu’à l’échelle globale de l’Inde du sud, cette autocorrélation spatiale est minimale et que les variations observées dans le sex-ratio enfantin pourraient être en grande partie spatialement aléatoires. Ce qui suggère que la distribution même de ces valeurs serait aléatoire, comme cela est précisément observé parmi les populations qui ne pratiquent pas de sélection sexuelle active (les variations étant alors liées principalement à des variations, modestes, du sex-ratio à la naissance).

Cette conclusion souligne en même temps les limites de l’indice de Moran global, qui sur l’ensemble régional ne fait état que d’un degré modeste de structuration spatiale alors que la concentration des déséquilibres en faveur des garçons est particulièrement marquée en certaines zones. On verra plus loin comment le « Moran local » permet de porter un regard plus précis sur les variations sous-régionales, indépendamment de la structure spatiale d’ensemble.

3.2.   Les principales dimensions : autocorrélation spatiale et niveau d’agrégation

Notre agrégation en famille de clusters de taille croissante permet en outre un examen original. Une question récurrente de l’analyse géographique est en effet la prise en compte de l’effet d’échelle. Au-delà de ce principe général, une forte mise en garde forte découlant des travaux de l’analyse spatiale vise notamment la dépendance scalaire : un même phénomène se lirait différemment à différentes échelles. Les géographes évoquent alors le MAUP (modifiable areal unit problem) : les variations d’échelle ou de découpage (zonage) peuvent influer sur la mesure d’un phénomène. Nous pouvons ici examiner de plus près la dimension proprement scalaire du problème, puisque nous disposons de cinq échelles différentes (auxquelles on pourrait même adjoindre les échelles administratives). On notera en outre que nos échelles successives ont la propriété inhabituelle de ne pas être emboîtées géométriquement: les clusters à 2 km ne correspondent pas aux clusters à 5 km et ainsi de suite (voir les cartes précédentes) Ceci garantit à chaque échelle une complète indépendance de construction vis-à-vis des autres échelles.

La question que nous allons poser est de savoir si l’autocorrélation spatiale mesurée est fonction de l’échelle choisie. Plus précisément, on se demandera si et comment le fait d’avoir agrégé modifie le calcul de l’autocorrélation spatiale. Pour répondre à cette question, nous nous proposons de procéder à un calcul de l’indice de Moran sur une même variable pour différentes familles de clusters. Nous avons choisi ici de résumer nos résultats en utilisant une seule variable, à savoir le rapport enfants-femmes (REF), indicateur indirect de la fécondité déjà utilisé pour nos illustrations et dont la structuration spatiale est très accentuée (voir plus haut). En revanche, nous butons à nouveau sur des problèmes de calculabilité pour les échantillons de taille excessive: villages d’origine (70.000 unités habitées) et cluster à 2 km (24.000 unités).

Comme nous l’avons évoqué précédemment, ces volumes déterminent des matrices de proximité de taille considérable, respectivement de 2 milliards et 280 millions de paires d’observations. Pour résoudre cette difficulté, nous avons choisi de calculer les résultats sur des échantillons aléatoires : 10% des villages d’origine et 25% des clusters de 2 km. Cette méthode souligne naturellement des questions particulières sur l’échantillonnage spatial[11] que nous n’aborderons pas ici, faute de place. Les calculs intermédiaires ont toutefois montré que la variation des tirages aléatoires était sans effet sensible sur les résultats. La Figure 8 représente le nombre de paires d’observations traitées (en unités logarithmiques) et on en dénombre plusieurs dizaines par classe de distance dans la plupart des cas, ce nombre de paires d’observations dépassant le million pour les clusters de petite taille qui sont plus nombreux.

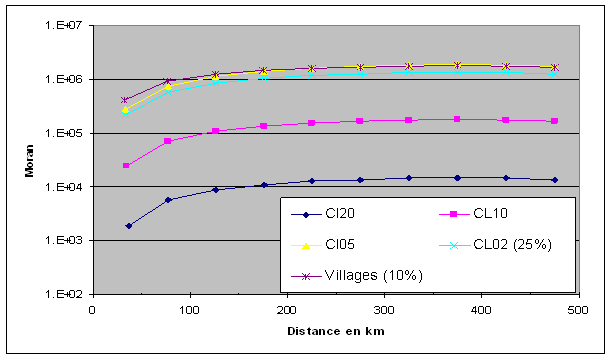
Figure 8 : Paires d’observations par pas de 50 km pour différentes familles d’agrégation et les villages d’origine (échantillonnage indiqué entre parenthèses)

Afin d’homogénéiser, nous avons conservé les mêmes pas de distance pour toutes les échelles de calcul, même s’il aurait été possible d’utiliser des pas de distance beaucoup plus court pour les petits clusters ou les villages d’origine. Les résultats sont présentés sur la Figure 8 qui reprend les indices de Moran pour les différentes familles d’agrégation. Ils indiquent des niveaux très élevés d’autocorrélation spatiale qui vont déclinant avec la distance croissante, de manière linéaire (ce qui suggère un étalement particulièrement régulier des valeurs). On distingue aussi clairement une hiérarchisation évidente de l’autocorrélation spatiale : les différentes courbes se superposent à partir des courtes distances de manière très régulière et sans chevauchement, l’agrégation progressive ayant pour effet d’augmenter graduellement le niveau d’autocorrélation spatiale. Les valeurs de l’indice de Moran sont particulièrement élevées pour les fortes agrégations, atteignant ainsi 0.8 pour les clusters à 20 km qui sont voisins immédiats (moins de 50 km de distance). On observe également que les courbes d’indices de Moran se rejoignent toutes pour les classes de distance 400-450 km à un niveau presque nul : la structuration d’intensité variable selon l’échelle manifeste néanmoins un profil comparable dans son étalement et sa portée.

Un examen plus fin de la courbure des mesures indique en outre un léger décrochement entre la première classe de distance et les suivantes que l’on observe en parallèle sur les différentes courbes. La nature de cette anomalie mériterait un examen spécifique, mais un premier survol de la mesure par classes de distance plus fines (Figure 9) suggère l’existence d’une première courbure concave à faible distance, suivie par une progression plus rectiligne pour des distances plus grandes.

Notons enfin le statut particulier des premiers niveaux d’agrégation, à savoir les données brutes et les clusters à 2 km. On note un décalage marqué avec les niveaux d’autocorrélation spatiale des autres échelles et ceci est notamment vrai des unités villageoises d’origine, dont le niveau d’autocorrélation spatiale est très médiocre. Il plafonne à 0.22 et les tests faits à partir d’autres échantillons à 10% fournissent des résultats de cet ordre.

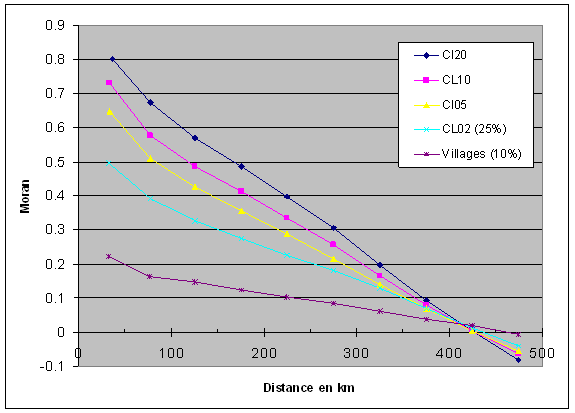
Figure 9 : Indice de Moran (REF) calculé sur des pas de 50 km pour différentes familles d’agrégation et les villages d’origine (échantillonnage indiqué entre parenthèses)

L’interprétation de ces résultats débutera par les données villageoises, dont on relèvera le faible degré d’autocorrélation spatiale. On peut de ce fait avancer comme première hypothèse que la variabilité statistique propre aux données villageoises a un effet considérable sur l’intensité de l’autocorrélation spatiale au point de la neutraliser en grande partie. Ce « bruit statistique » pourrait tenir en partie aux faibles effectifs de nombreuses localités, pour lesquelles le calcul du REF est instable. Mais il est également possible d’y lire la trace d’une micro-variabilité réelle de la fécondité mesurée localement par le REF : les différentes entre villages voisins correspondent alors à des variations effectives de fécondité entre localités en dépit du gradient géographique.

Il n’est pas aisé d’établir formellement que les défaillances statistiques des données dans les petites localités jouent un rôle majeur dans la faible autocorrélation mesurée à l’échelle villageoise, mais le graphique qui suit fournit un élément partiel de preuve. On y a en effet superposé les résultats précédents pour les villages et les clusters, ainsi que pour deux autres échantillons de villages : les villages de moins de 1000 habitants et ceux de plus de 1000 habitants, découpage partageant l’échantillon en deux et dont le seuil s’inspire également des observations sur la variabilité des données selon la taille démographique des unités considérées (voir Guilmoto et al. 2004). Le tirage aléatoire porte désormais sur 20% de l’échantillon total. Cette comparaison est éclairante. On constate en effet que l’autocorrélation spatiale des gros villages est très largement supérieure à celle des petits villages, ces derniers se caractérisant par les plus faibles valeurs de Moran. La valeur maximale plafonne désormais à 0.17 pour les villages les moins peuplés contre 0.46 pour les autres villages. Concernant les villages les plus habités, on notera en outre que leur niveau d’autocorrélation spatiale est très comparable à celle des clusters à 2 km, voire plus élevés pour les distances supérieures à 100 km. On rappellera que les clusters à 2 km ont en moyenne une population de 5700 habitants, mais comptent toujours, en dépit de l’agrégation opérée, plus de 8.5% d’unités dont la population totale est strictement inférieure à 1000 habitants : ces clusters pourraient donc contribuer à faire baisser le niveau de l’indice de Moran. Les villages de plus de 1000 habitants ont pour leur part une population moyenne de 3700 habitants, mais par définition une population minimale de 1000 habitants au moins.

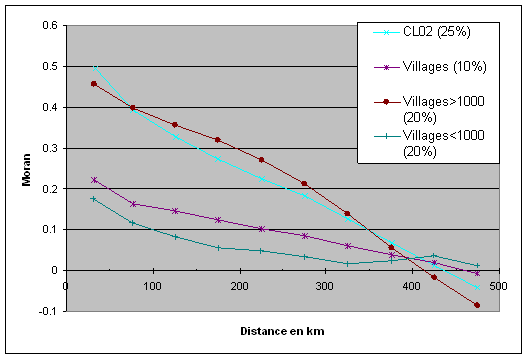
Figure 10 : Indice de Moran (REF) pour les villages et les clusters de 5 km

Si nous ne pouvons tirer de conclusion formelle de cette analyse[12], les enseignements préliminaires semblent indiquer que l’effet propre au bruit statistique dû à la faiblesse des effectifs est considérable sur le calcul de l’autocorrélation spatiale. En l’absence de villages « sous-peuplés », l’autocorrélation spatiale serait vraisemblablement analogue à celle obtenue sur une agrégation à 2 km. Une autre composante potentielle de la faible autocorrélation spatiale à l’échelle villageoise évoquée plus haut, à savoir la micro-variabilité du REF entre localités, serait alors modeste puisqu’on constate que le premier niveau d’agrégation n’améliore pas notablement l’autocorrélation spatiale dès lors que la taille des villages est suffisante. Il s’agit toutefois d’une hypothèse à explorer de manière plus systématique en raison de biais possibles d’échantillonnage dans les différents cas.

Les autres distributions des indices de Moran représentées sur la figure 9 correspondent à présent à des échantillons exhaustifs et à des unités statistiques de taille conséquente ; on ne peut postuler un effet propre aux effectifs ou aux tirages. Il ressort de cette comparaison en premier lieu que le niveau de structuration spatiale est très élevé pour les trois échelles. On observe en outre que l’agrégation a pour effet de rehausser l’autocorrélation spatiale de manière sensible, puisqu’elle passe pour le premier rang de distance de 0.64 (cluster 5 km) à 0.73 (cluster 10 km), puis 0.80 (cluster 20 km). Ceci suggère des tendances micro-régionales de fécondité à distribution spatiale irrégulière que l’agrégation croissante gomme progressivement. Ces irrégularités spatiales détectées pourraient être de différente nature, résultant d’une hétérogénéité du peuplement (par exemple, de la population féminine alphabétisée ou active), responsable de variations de fécondité ou bien encore d’une dimension intrinsèquement hétérogène des comportements de fécondité régionaux. Il demeure que cette dimension est largement inférieure au niveau d’autocorrélation spatiale partagée par les trois familles d’agrégation supérieure, qu’on peut évaluer au niveau d’autocorrélation spatiale minimal mesuré pour les clusters à 5 km.

---