Espace et mesure en Inde du Sud (EMIS)

3.3.   Les principales dimensions : autocorrélation spatiale locale (LISA)

La limite de l’exploration des données spatiales par des indices globaux d’autocorrélation spatiale est ici atteinte. L’apport du variogramme nous a permis d’aller plus loin, puisque nous avons pu mesurer le degré de structuration spatiale. Nous ne sommes néanmoins pas en mesure de connaître le détail de la structure spatiale de la variable étudiée (ce point est déjà souligné par Charre, 1995 :82). D’ailleurs, c’est de cette manière que peut être comprise l’objection à l’utilisation du concept d’autocorrélation spatiale formulée par Brunet & Dollfus (1990 : 87). En effet, le point souligné est surtout l’absence de variables totalement autocorrélées spatialement (mais à l’inverse aussi absolument pas autocorrélées). Sans le dire explicitement, les auteurs soulignent l’incapacité des indices de l’époque à aller plus dans le détail.

Sauf à avoir des gradients continus, phénomène assez rare en sciences sociales, comprendre la structure spatiale des phénomènes nécessite ainsi de pouvoir accéder à une information plus locale. En effet, les indices généraux peuvent être « aveugles » face à des phénomènes très fortement structurés, mais sur de petites zones au sein d’un espace absolument pas structuré. C’est par exemple le cas du rapport de féminité des enfants, dont on a montré ailleurs la forte structuration spatiale à l’échelle des deux districts de Salem et Dharmapuri (voir Figure 11), mais qui à l’échelle du Tamil Nadu n’offre aucune structure spécifique. Comparer la carte avec le variogramme (dont les valeurs sont nulles) est, de ce point de vue, instructif sur les limites de cette approche. Une solution consiste alors, comme nous l’avons fait précédemment, à mettre en perspective les informations issues des variogrammes avec la cartographie des variables. Mais l’approche redevient assez empirique, voire ad hoc.

Une démarche permettant de dépasser cet état de fait serait de pouvoir inspecter pour chaque point son niveau de ressemblance avec ses voisins. Ainsi, on pourrait mettre en valeur des zones où le niveau de ressemblance local est important, et utiliser cette information pour envisager une étude désagrégée de la structure spatiale des phénomènes. Il s’agirait en quelque sorte d’une mesure locale de l’autocorrélation spatiale, par opposition aux mesures globales.

Arrivés à ces mêmes conclusions concernant l’incapacité des indices globaux à prendre en compte les structures spatiales fines, plusieurs chercheurs anglo-saxons ont travaillé à l’élaboration de nouveaux indices, capables de rendre compte de l’autocorrélation spatiale à une échelle locale. Les résultats les plus notables sont les statistiques G_i et G^*_i (Getis, Ord, 1992), l’indice de Geary local et l’indice de Moran local (Anselin, 1995). Le Tableau 4 propose un récapitulatif des indices permettant de mesurer le niveau d’autocorrélation spatiale distingué en fonction de leur forme statistique (colonnes) et de leur échelle d’application (lignes).

Tableau 4 : Taxonomie des indices d’autocorrélation spatiale (d’après Getis, Ord, 1992 : 263)

Type	Produits croisés	Différences (au carré)
Global, mesure simple	Moran	Geary
Global, différents pas de distance	Corrélogramme	réagrégation
Local, différents pas de distance	Gi, G*i, Moran local	Geary local

Les indices locaux mettent en évidence des associations locales de valeur. Le terme d’association locale apporte une légère nuance à celui d’autocorrélation spatiale locale. Quand l’autocorrélation spatiale mesure la plus grande similarité statistique des valeurs de deux individus entre eux que par rapport à la moyenne de l’échantillon, le terme d’association soulignerait plutôt le regroupement spatial des individus de valeurs extrêmes. La nuance est faible, et les deux termes sont généralement employés comme synonymes.

Néanmoins, l’utilisation du terme association indique aussi la finalité de ces indices : mettre en valeur des sous espaces aux caractéristiques similaires, qui se distinguent de la moyenne de l’échantillon observé (on le verra lorsque sera abordée la forme mathématique de ces indices). Le terme décrivant ces zones est celui de « point chaud » (hot spots). Le point chaud, nous rappelle Le Robert, est un « lieu où il se passe quelque chose ». On retrouve l’idée de concentration locale par rapport à un ensemble général.

C’est donc tout logiquement que les projets qui ont porté ces recherches, depuis la fin des années 1990 jusqu’à aujourd’hui, ont été financés par des institutions publiques de santé ou de justice[13]. En effet, l’épidémiologie et la criminologie, disciplines appliquées et bien financées, sont clientes d’étude à dimension fortement spatiale pour affiner leur compréhension des phénomènes et améliorer leurs prédictions. La diffusion est au centre des travaux de la première, la concentration au cœur de la seconde. Dans ce dernier cas, les points chauds prennent un double sens, celui de concentration, mais aussi celui de zone dangereuse. C’est sans surprise qu’un des premiers logiciels gratuits permettant de calculer des indices locaux d’autocorrélation spatiale se nomme « Crimestat » (Levine, 2002 ; la première édition du logiciel date de 1999).

3.3.1.      Saisir les structures localement

[14]. En effet, puisque cette statistique gamma est une somme pour tous les « i », on peut définir pour chaque individu « i » un gamma local de la forme :

On voit bien la relation qui unit un indice gamma local à l’indice global : l’indice global est la somme de tous les indices locaux.

Un facteur de proportionnalité  peut éventuellement être introduit, cela ne change pas la relation : .

Cette particularité permet d’apprécier la valeur d’un gamma local en fonction du gamma global. Ainsi, il est aisé de mettre en évidence des valeurs aberrantes, en comparant la valeur du gamma local à celle de la valeur de la moyenne des gammas locaux (c’est-à-dire le gamma global divisé par le nombre d’individus « i »).

Anselin propose ainsi la notion de Local Indicators of Spatial Association (LISA), terme générique regroupant différents indices qui permettent de mesurer l’autocorrélation spatiale locale. Cet acronyme sera rapidement repris par les autres auteurs (Getis, Ord, 1996, Bao, Henry, 1996). Pour Anselin (1995 : 94), « un indicateur local d’association spatiale est n’importe quelle statistique répondant à deux critères :

a)      Le LISA de chaque observation donne une indication sur l’étendue d’un regroupement spatial significatif de valeurs similaires autour de cette observation.

b)      La somme des LISA pour toutes les observations est proportionnelle à un indicateur global d’association spatiale. »

Un LISA est donc un indice qui permet de mesurer localement l’autocorrélation spatiale et dont la somme pour tous les individus donne le niveau d’autocorrélation spatiale global de la variable dans l’espace étudié. La supériorité des LISA sur d’autres méthodes, comme les statistiques G_i et G^*_i, est ici marquée : les premiers permettent un aller-retour entre le local et le global, alors que les secondes ne proposent que la mise en évidence des points chauds. On rappellera enfin que les LISA ont deux fonctions complémentaires. La première est la mise en valeur des regroupements locaux de valeurs similaires (spatial clustering), particulièrement dans les cas où l’autocorrélation spatiale globale est nulle. La seconde leur permet de mettre en évidence une instabilité locale lorsque l’autocorrélation spatiale globale existe (les outliers dans les grandes tendances).

3.3.2.      Introduction aux LISA : l’indice de Moran local et son utilisation

Ces LISA vont nous permettre de mettre en évidence la structure des indices étudiés à l’échelle de l’Inde du Sud. Nous utiliserons pour cela la version locale de l’indice de Moran (indice le plus répandu et le mieux maîtrisé, comme nous l’avons précisé précédemment).

 

L’Indice de Moran est bien une statistique gamma, puisque si l’on remplace « v_ij » par  , on obtient bien la formule générale de l’indice de Moran présentée précédemment (après standardisation en ligne).

L’indicateur local (ou « Moran local ») est donné par la formule :

 

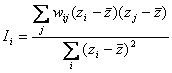
Conformément à la règle, la somme des indices de Moran locaux est proportionnelle à l’indice de Moran global : , avec .

Ce facteur de proportionnalité retenu n’est valable que si les variables sont standardisées et si la matrice de pondération est standardisée en ligne (ce qui est notre cas). Son principal intérêt est de proposer alors une relation simple et pratique de la proportionnalité entre indice global et indice local. En effet, la moyenne des indices locaux est alors égale à l’indice global. Il sera donc possible de proposer pour des sous espaces des indices de Moran globaux qui seront la moyenne pour ces sous espaces des indices locaux, et qui pourront être comparés à l’indice global pour l’ensemble du Tamil Nadu, mais aussi entre eux.

C’est aussi grâce à ce lien de proportionnalité que l’on peut obtenir pour chaque village une estimation de sa ressemblance avec les villages voisins par rapport à sa ressemblance à l’ensemble des villages, et tester la significativité de cette ressemblance. On distingue alors quatre cas de figures[15] :

·        Les villages avec un indice fort dans un voisinage qui lui ressemble (autocorrélation spatiale positive et valeur de l’indice élevé). Situation résumée en « plus-plus » (high-high).

·        Les villages avec un indice fort dans un voisinage qui ne lui ressemble pas (autocorrélation spatiale négative et valeur de l’indice élevé). Situation résumée en « plus-moins » (high-low).

·        Les villages avec un indice faible dans un voisinage qui lui ressemble (autocorrélation spatiale positive et valeur de l’indice faible). Situation résumée en « moins-moins » (low-low).

·        Les villages avec un indice faible dans un voisinage qui ne lui ressemble pas (autocorrélation spatiale négative et valeur de l’indice faible). Situation résumée en « moins-plus » (low-high).

On a ainsi une indication sur le niveau d’autocorrélation spatiale (comme pour les indices globaux) mais aussi une information sur le type d’association présente.

On comprend mieux aussi pourquoi le niveau d’autocorrélation spatiale augmente lorsque l’on agrège les données. En effet, si l’on considère qu’un indice global est la somme des indices locaux, plus les indices locaux sont autocorrélés, plus le niveau global d’autocorrélation spatiale sera élevé. Or, plus la maille étudiée est fine, plus on a de chance d’avoir des valeurs extrêmes (outliers). Ou plutôt, plus on agrège les données, plus les valeurs extrêmes présentes localement sont absorbées dans des mailles de taille supérieure où la tendance domine. Ainsi, c’est la tendance dominante qui l’emporte, et les valeurs aberrantes disparaissent, renforçant l’autocorrélation spatiale globale. Sans approfondir ici le questionnement sur le MAUP[16] (Modifiable Areal Unit Problem - problème des surfaces aréolaires variables), on doit néanmoins envisager les LISA comme une nouvelle piste d’exploration de ce problème inhérent à l’utilisation de données géographiques basées sur des mailles de taille inégale. Dans le même ordre d’idée, Amrhein et Reynolds (1996) proposent une exploration des effets de l’agrégation des données à partir des statistiques G_i.

3.4.   Interpréter les LISA

Avant d’aller plus loin, il convient de revenir sur un point technique, celui de la significativité des indices calculés localement.

3.4.1.      Significativité de l’indice de Moran local

Comme pour des indices généraux de corrélation (spatiale ou non), il est possible de connaître le niveau de fiabilité (significativité) de l’indice de Moran local. La significativité exacte de l’indice calculé peut être approximée, mais la mise en œuvre de ce type de calcul est trop complexe. Anselin (1995 : 99) montre en effet que l’on peut construire un test de significativité en s’appuyant sur le 4^ème moment de l’indice local de Moran. Il rappelle cependant que la distribution exacte de cette statistique est encore inconnue. De plus, il rappelle (p. 108) que ces distributions pourraient être connues sous l’hypothèse d’autocorrélation spatiale globale nulle, ce qui est rarement le cas. Pour plus de détails, on consultera les travaux de Michael Tiefelsdorf (plus particulièrement Tiefelsdorf & Boots, 1997 et Tiefelsdorf, 1998).

C’est pourquoi les différents auteurs préfèrent utiliser une randomisation conditionnelle grâce à un test de Monte Carlo pour évaluer la significativité des statistiques locales (Moran local, Geary local, statistiques G). Ce test consiste à prendre les valeurs réelles (ce qui constitue la condition) des voisins de chaque point, et de les mélanger aléatoirement (randomisation) pour voir si l’indice calculé est dû ou non au hasard. L’opération est répétée un certain nombre de fois afin de calculer une probabilité. Celle-ci est exprimée en pourcentage. On peut cartographier cette probabilité et la comparer à la distribution des valeurs de l’indice.

Sans s’attarder encore sur la répartition des zones où l’indice est significatif (voir sur la Figure 11), on notera cependant que les espaces où il n’est pas significatif semblent se placer en "tampon" entre des zones d’autocorrélation spatiale positive et des zones d’autocorrélation spatiale négative. On remarquera aussi que le niveau de significativité est organisé autour d’un centre de valeurs fortement significatives. Cette organisation suggère une première lecture en termes de degré d’hétérogénéité. Ainsi les zones blanches (non significatives) recouvrent deux types d’unités, lesquelles peuvent d’ailleurs coexister. Les premières ressemblent au village moyen et ont donc des valeurs proches de la moyenne, ce qui leur confère une autocorrélation spatiale locale faible (puisque leur écart à la moyenne est réduit), alors même qu’il peut s’agir de zones homogènes. Les secondes ont des valeurs d’autocorrélation spatiale locale variée, mais dans un voisinage où les valeurs d’autocorrélation spatiale locales sont hétérogènes. Il en résulte qu’après un test par randomisation, on ne peut pas dégager de tendance locale, positive ou négative (d’où l’absence de significativité). La somme des indices de Moran locaux calculés localement est donc nulle.

3.4.2.      Interprétation

Les informations disponibles pour chaque village sont maintenant de trois ordres. Elles concernent les valeurs de la variable, le niveau local d’association spatiale (la valeur de l’indice local de Moran), et l’intervalle de confiance (le niveau de significativité). En couplant ces trois données, on peut obtenir une vue synthétique de la distribution des valeurs à l’échelle de l’Etat en séparant les villages selon leurs caractéristiques.

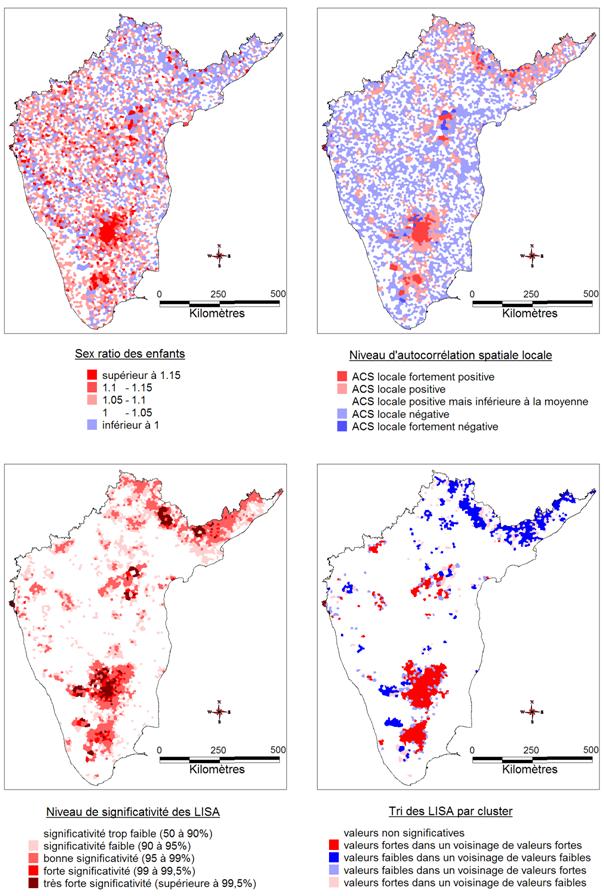
Figure 11 : 3 en 1, la carte des clusters de LISA. Un exemple avec le sex ratio des enfants

On va ainsi trouver d’abord des villages dont les valeurs de LISA sont non significatives. Ces villages seront exclus du reste du traitement. On trouvera ensuite des valeurs autocorrélées positivement et des valeurs autocorrélées négativement. Chacun de ces deux groupes pourra être divisé selon la valeur originale de l’indice : supérieur ou inférieur à la moyenne. On crée ainsi quatre catégories, qui renvoient au nuage de points de Moran présenté en annexe (voir à la fin) :

·        Les valeurs positives (indice supérieur à la moyenne) au sein d’un environnement de points à valeur positive (autocorrélation spatiale positive). Association qualifiée de high-high dans la littérature anglo-saxonne.

·        Les valeurs négatives (indice inférieur à la moyenne) au sein d’un environnement de points à valeur négative (autocorrélation spatiale positive). Association qualifiée de low-low.

·        Les valeurs positives au sein d’un environnement de points à valeur négative (autocorrélation spatiale négative). Association qualifiée de high-low.

·        Les valeurs négatives au sein d’un environnement de points à valeur positive (autocorrélation spatiale négative). Association qualifiée de low-high.

La Figure 11 présente la combinaison de trois cartes (valeurs de l’indice, valeurs locale du niveau d’autocorrélation spatiale et niveau de significativité de l’autocorrélation spatiale locale) pour en obtenir une quatrième qui les synthétise.

On met ainsi en valeur des poches d’autocorrélation spatiale positive, qui sont liées à des regroupements de valeurs fortes (ici représentées en rouge foncé) ou de valeurs faibles (en bleu foncé). A contrario, on isole aussi des éléments isolés dans un voisinage homogène. Ce sont des villages dont les valeurs tranchent avec leur voisin, et que l’on peut qualifier de valeurs spatialement atypiques (spatial outliers) car elles ne suivent pas la tendance locale. Ils sont représentés en rose pour les valeurs fortes dans des régions de faible modernisation, et en bleu clair pour les valeurs faibles dans les régions de forte modernisation.

Appliqués à des phénomènes qui sont globalement peu autocorrélés, comme c’est le cas du sex-ratio des enfants, les LISA permettent de révéler des sous espaces qui pourraient être autocorrélés (Figure 11, carte des clusters de LISA : au sud, on voit nettement deux poches importantes de sex-ratio déficitaires pour les petites filles).

Face à des phénomènes fortement autocorrélés, la cartographie des LISA permet de mieux comprendre la structure locale des données. Par exemple, si l’on s’intéresse à l’alphabétisation (Figure 12), on voit bien la distribution des zones peu alphabétisées et l’importante homogénéité des zones où elles se situent permettant de souligner l’aspect régional de la faible alphabétisati

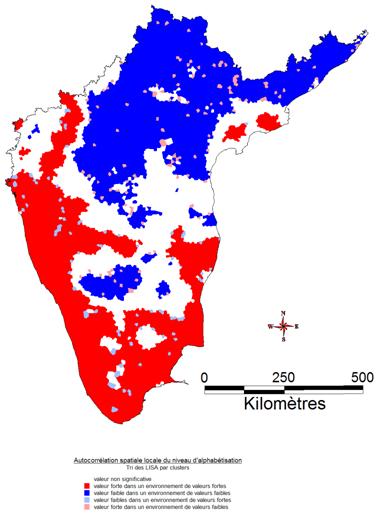
Figure 12 : autocorrélation spatiale locale de l’aphabétisation.

3.4.3.      Une réflexion à propos des échelles

Il est intéressant de souligner que la portée du voisinage définie pour mesurer l’autocorrélation spatiale influe directement sur la perception que l’on peut avoir du phénomène. Ainsi, si nous avons remarqué précédemment que le niveau d’autocorrélation spatiale global variait en fonction de la distance entre les points, on peut mettre en valeur les changements de structure de l’autocorrélation spatiale globale en cartographiant les niveaux d’autocorrélation spatiale locaux pour différents voisinages.

C’est ce que nous montre la Figure 13, qui présente pour l’alphabétisation la mesure de l’autocorrélation spatiale locale en fonction d’un voisinage de 25, 50 puis 100 kilomètres. On comprend mieux ainsi pourquoi l’autocorrélation spatiale globale tend à diminuer, puisqu’elle passe de 0,82 pour un voisinage de 25 km à 0,76 pour un voisinage de 50 km, et enfin à 0,64 pour un voisinage de 100 km[17]. En effet, au fur et à mesure que la distance augmente, le nombre de voisins pris en compte augmente, ce qui tend à définir des régions toujours plus grandes, mais dont l’hétérogénéité interne augmente. De facto, l’indice de Moran, qui mesure cette hétérogénéité tend à diminuer. On le voit d’ailleurs sur les figures avec l’augmentation du nombre de clusters ayant des valeurs spatialement atypiques (en bleu clair et en rose) lorsque la distance du voisinage augmente. Nous devons donc souligner ici l’importance à accorder à l’étude préliminaire du choix de la distance de voisinage. Par ailleurs, la mesure locale de l’autocorrélation spatiale se révèle un outil précieux pour comprendre l’organisation des phénomènes sociaux à différentes échelles.

Figure 13 : autocorrélation spatiale de l'alphabétisation selon trois définitions du voisinage.

 

---