Annexe I : Le nuage de points de Moran

Le nuage de points de Moran est décrit en détail dans Anselin (1996), il est aussi évoqué dans Anselin (1995 & 2003). Il s’agit d’un mode de visualisation des données statistiques spatiales. Anselin fait le constat en 1996 que si les techniques consistant à « laisser les données parler d’elles-mêmes » (Gould, 1981) s’étaient bien développées (voir par exemple Monmonnier, 1989) depuis les travaux de Tukey (1977) et la mise en valeur des techniques d’EDA (analyse exploratoire des données), il n’en était pas de même pour l’analyse exploratoire des données spatiales (ESDA).

Fort de la mise en place des indices locaux d’association spatiale (LISA), Anselin propose une autre innovation, qui leur est liée, sans toute fois être identique. Comme il le rappelle lui-même : « le nuage de points de Moran n’est pas un LISA » (Anselin, 1995 : 105).

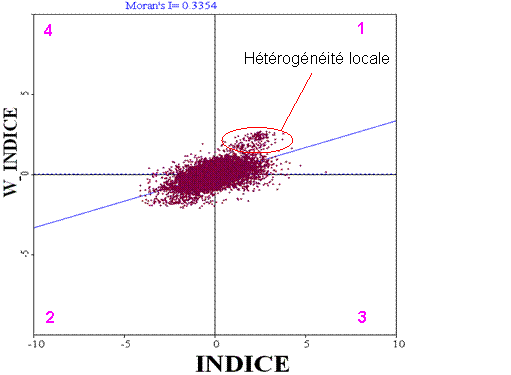
Figure 34 : nuage de point de Moran pour l’indice de modernisation (voisinage de 15 km)

Le principe de ce nuage de points est assez simple. Il consiste à mettre en opposition la valeur d’une variable en un point « i » et sa valeur dans son voisinage « j » (voisinage défini par une matrice w_ij,), après avoir normalisé et standardisé les variables. En répétant l’opération pour tous les points « i » et leurs voisins « j », on obtient un nuage de points qui nous permet de visualiser à la fois l’autocorrélation spatiale de la variable et son hétérogénéité.

L’autocorrélation spatiale est déduite de la pente de la droite de régression (en bleu sur la figure) entre les valeurs en « i » (INDICE) et en « j » (W_INDICE), soit 0,3354 dans l’exemple présenté. Les zones d’hétérogénéité locale (poches où l’autocorrélation spatiale est plus forte ou plus faible que dans l’ensemble de l’échantillon) sont mises en valeur par des regroupements visibles sur le nuage de points. On voit, entourées en rouge sur la figure, des valeurs de voisinages plus fortes que la moyenne des valeurs des voisinages, qui correspondent à la poche au Sud du Tamil Nadu.

On peut aussi distinguer quatre types d’associations qui correspondent aux quatre quadrants du nuage de points de la Figure 34:

·        Les valeurs positives (indice supérieur à la moyenne) au sein d’un environnement de points à valeur positive (autocorrélation spatiale positive). Association qualifiée de high-high dans la littérature anglo-saxonne sont visibles dans le quadrant n°1 (chiffre en rose).

·        Les valeurs négatives (indice inférieur à la moyenne) au sein d’un environnement de points à valeur négative (autocorrélation spatiale positive). Association qualifiée de low-low. Ils sont visibles dans le quadrant n°2.

·        Les valeurs positives au sein d’un environnement de points à valeur négative (autocorrélation spatiale négative). Association qualifiée de high-low. Ils sont visibles dans le quadrant n°3.

·        Les valeurs négatives au sein d’un environnement de points à valeur positive (autocorrélation spatiale négative). Association qualifiée de low-high. Ils sont visibles dans le quadrant n°4.

On comprend ainsi mieux que les points situés dans les quadrants 1 et 2 participent à la tendance rendant l’autocorrélation spatiale positive, alors que les points situés dans les quadrants 3 et 4 tendent à rendre l’autocorrélation spatiale négative. Les points situés dans ces deux quadrants sont qualifiés de « spatial outliers » (valeurs spatialement atypiques), puisqu’ils ont des valeurs opposés à celles de leurs voisins.

Annexe II : Le cokrigeage

La méthode du cokrigeage n’a guère été utilisée dans l’analyse de la pauvreté. Pour la décrire en quelques mots, on dira que cette technique consiste à compléter un krigeage pour estimer des données locales à partir d’estimations éparses de données complémentaires, disponibles à l’échelle locale. Le cokrigeage associe en effet un krigeage d’une variable z (disponible à une échelle donnée) à une modélisation statistique de la même variable z grâce à un vecteur x de covariables différentes de z,  mais disponibles à une échelle locale plus fine. La modélisation statistique permet de mieux estimer les micro-variations de z par imputation à partir du vecteur x, tout en conservant les propriétés du krigeage comme estimateur spatiale[35].

Cette méthode nous a semblé pourtant cruciale pour importer localement des données disponibles à une échelle supérieure et mériterait d’être systématisée à ce genre d’exercice. Elle n’est à notre connaissance que rarement utilisé en science sociale.[36] Nous allons en premier lieu résumer notre problème d’estimation et examiner les différentes solutions disponibles et leurs avantages respectifs.

Nous disposons ici d’une estimation de la mortalité infantile rurale à l’échelle des 80 districts de l’Inde du sud (en 1991). Nous aimerions disposer d’estimation géographiquement plus fines, applicables par exemple à nos clusters (cl05 ou cl10). Il s’agit d’un cas relativement classique d’imputation macro->micro. Les districts sont les unités macro et les clusters sont les unités micro.

• Sources macro : mortalité infantile, covariables du recensement
• Sources micro : covariables du recensement
• Informations spatiales : localisations micro et macro
• Objectif : estimation micro de la mortalité infantile

Différentes méthodes se présentent que nous résumons dans la liste qui suit :

1.      Imputation uniforme : toutes les unités micro prennent la valeur de l’unité macro

2.      Krigeage : krigeage sur les unités micro des valeurs macro, attribuées au centre de l’unité macro

3.      Imputation statistique : modélisation macro du lien entre la valeur observée et d’autres covariables. Application micro du modèle obtenu aux mêmes covariables disponibles, pour obtenir une estimation micro.

4.      Cokrigeage : krigeage (cf. plus haut) en tenant compte des mêmes covariables macro (modélisation) et micro (imputation)

Les avantages et désavantages respectifs sont également résumés :

1. Simplicité absolue de la méthode. Mais résultat uniforme sans distinction micro.
2. régularité spatiale de l’estimation. Mais centralité de l’estimation et lissage en partie artificielle entre centroïdes
3. Imputation micro détaillée grâce aux covariables. Mais résultat aspatial et forte sensibilité à la qualité de la donnée micro
4. Combinaison des avantages des deux précédents : estimation spatialement régulière et maximisation de l’usage des covariables micro. Mais effet de centralité du krigeage et sensibilité à la qualité de l’information micro.

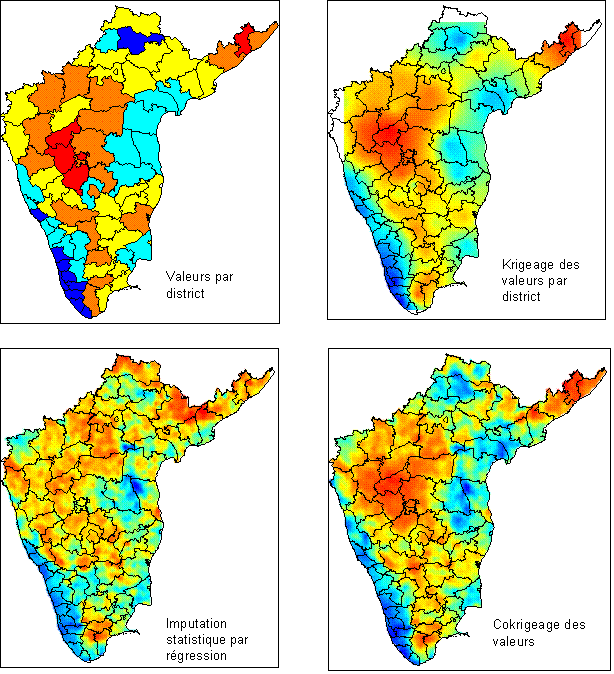
Figure 35 : Estimation locale de la mortalité infanto-juvénile selon quatre méthodes : uniformité au sein des districts, krigeage de la valeur district, imputation locale, cokrigeage

Notons que pour rendre opérationnelle les deux dernières méthodes 3 et 4, nous avons choisi une batterie de variables liées à la mortalité infantile. Ces dernières ont été examinées par ajustements successifs afin d’éliminer l’effet de variations « aberrantes » à l’échelle micro. Considérons par exemple l’effet d’une variable à faible variation macro, comme la présence de tribaux, variant de 0 à 15% dans les districts. Cette variable peut avoir un lien statistique, faisant par exemple monter la mortalité. L’équation liant la mortalité à ses covariables, parmi lesquels la proportion de tribaux, a toutefois été calibrée à partir d’observations macro à faible écart-type. Or, si au sein d’un cluster on trouve un pourcentage atypique de tribaux (disons 100%), cela peut faire entièrement basculer l’imputation et décupler la mortalité infantile. Le chiffre local devient proprement absurde et provient simplement de la présence d’une valeur extrême de la covariable, valeur non prise en compte dans la modélisation faite à l’échelle macro.

Nous avons donc dû éliminer les variables dont les variations locales étaient sans rapport avec les variations macro. A partir des covariables conservées, nous avons estimé la mortalité théorique macro et micro selon la méthode 3. Puis nous avons utilisé ces estimations comme base pour le cokrigeage. Sur la Figure 35, nous avons rassemblé les quatre méthodes. Les niveaux les plus élevés de mortalité infantile sont représentés ici en rouge, alors que les plus bas sont en bleu. Les points représentés correspondent aux centres des districts.

On reconnaît sur la première carte la distribution des valeurs par district. Aucune distinction à l’intérieur des districts n’est faite. La carte suivante est l’estimation par krigeage, dérivée de la précédente. Elle est centrée sur les centres de district qui servent de support à l’estimation surfacique. Les différences intra-district sont régulières.

Sur la troisième carte, l’imputation micro est faite à partir des covariables disponibles. La carte est alors beaucoup plus accidentée, car les variations locales affectent directement l’estimation. Elle ne correspond pas exactement avec la carte par district, en raison de l’imprécision de l’estimation.

La dernière carte de la Figure 35 est dérivée du cokrigeage. Elle correspond par conséquent à une reprise de la première carte obtenue par krigeage, mais avec une correction pour tenir compte des variations micro de la covariable et de l’intensité de la corrélation. Sans être très éloignée de la précédente, elle rétablit donc une plus forte régularité spatiale, à une échelle désormais plus fine que le krigeage originel, et les valeurs locales concordent mieux avec les moyennes de district de la première carte.

Pour donner une vue plus fine des particularités du cokrigeage, on a procédé à un zoom sur les cartes précédentes sur une partie de l’Inde du sud. Les deux cartes de la Figure 36 comparent donc les résultats par krigeage (à gauche) et cokrigeage (à droite) pour la région de Bangalore-Chennai, en utilisant toutefois une gamme chromatique légèrement différente pour faire ressortir les contrastes locaux. On distingue plus clairement le gain relatif au cokrigeage dans l’estimation des valeurs locales de la mortalité infanto-juvénile. La carte de gauche obtenue par krigeage fait en effet apparaître un profil très lisse, correspondant à une estimation presque linéaire de la mortalité entre les points d’observations, à savoir les valeurs par district.

La méthode du cokrigeage donne des résultats plus nuancés. A l’intérieur d’un district donné, les écarts entre localités sont marqués et irréguliers. L’estimation de ces écarts locaux repose naturellement sur les variations localement observées dans les covariables de la mortalité de notre modèle. On voit par exemple apparaître au sud de l’Andhra Pradesh côtier une petite poche à plus forte mortalité (en jaune) et les zones à fiable mortalité (en bleu) ont un découpage plus tourmenté.

Figure 36 : Estimation locale de la mortalité infanto-juvénile : krigeage et cokrigeage (zoom)

L’absence de données qui a justifié le cokrigeage initial ne nous permet naturellement de confirmer l’existence de ces micro-variations géographiques, mais les covariables de la mortalité (telle que le degré d’alphabétisation) fournissent sans doute des prédictions raisonnables. On voit ainsi apparaître sur la carte de cokrigeage une zone à faible mortalité (en bleu) sur le littoral du Tamil Nadu, absente de l’estimation initiale opérée par simple krigeage. Cette région n’est autre que la zone métropolitaine de Chennai, relativement prospère, où la mortalité est effectivement significativement inférieure à la moyenne locale. Inversement, le cokrigeage fait émerger de nouvelles poches à forte mortalité dans des régions longeant la frontière entre Tamil Nadu et Karnataka, qui correspondent effectivement à des régions semi-forestières de colline particulièrement déshéritées (région du fameux brigand Veerapan), où les conditions sanitaires sont très certainement plus médiocres que dans les plaines. On pourrait d’autres exemples qui semblent intuitivement plausibles, mais l’absence de données mesurées nous interdit d’aller plus loin.